Moyenne et médiane : définitions
Pour étudier une série statistique, il est utile d’en définir le « milieu », c’est-à-dire une valeur centrale. Pour cela, deux mesures mathématiques peuvent être utilisées : la moyenne et la médiane.
La moyenne est calculée comme la somme des valeurs d’une série divisée par le nombre de valeurs dans cette série. La médiane divise, quant à elle, la série étudiée en deux groupes égaux.
Moyenne et médiane : l’exemple des salaires en France
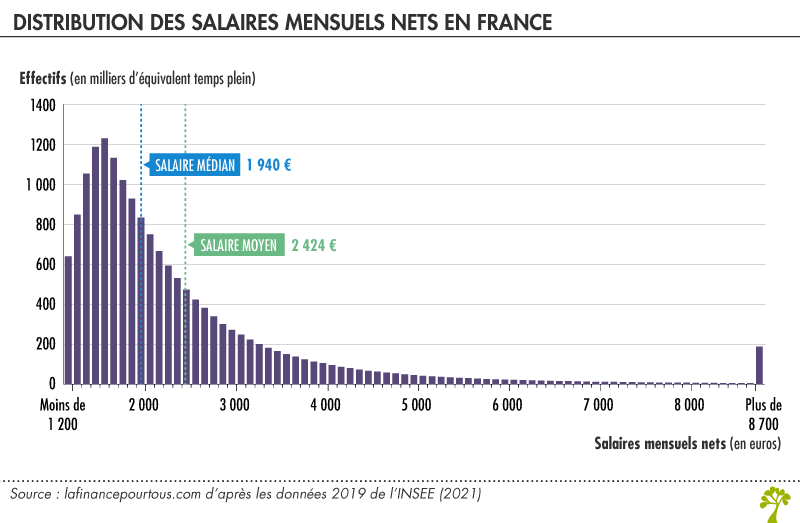
Prenons l’exemple des salaires. En France, en 2019, le salaire mensuel net moyen (en équivalent temps plein) était de 2 424 euros dans le secteur privé. Or, cette série contient de nombreuses valeurs extrêmes, c’est-à-dire éloignées de la moyenne. Par exemple, 1 % des employés du secteur privé ont un salaire supérieur à 9 103 euros par mois. Ces valeurs extrêmes gonflent ici, artificiellement, la moyenne et la rendent, d’une manière générale, peu représentative de la distribution effective des données.
Cet article et la vidéo associée (à retrouver ci-dessous) se fondent sur des données de 2019.
Dans ce cas, calculer la médiane est utile : le salaire mensuel net médian (en équivalent temps plein) était de 1 940 euros. Autrement dit, 50 % des salariés du secteur privé touchaient plus de 1 940 euros par mois et 50 % gagnaient moins. L’avantage de la médiane, par rapport à la moyenne, est d’être moins sensible aux valeurs extrêmes et ainsi d’offrir une donnée plus représentative de la réalité vécue par le plus grand nombre de salariés.
En résumé, la moyenne est une mesure utile dans l’étude d’une série statistique. En présence de nombreuses valeurs extrêmes, il est toutefois utile de calculer une médiane moins sensible à celles-ci.
Distinguer la moyenne de la médiane est également très utile dans l’étude de la distribution des patrimoines.





Très instructif . je vais m’en servir pour mes cours.
merci pour ce travail.
bien