Calculer le taux de rendement d’un placement grâce à la règle d’Einstein

Pour un épargnant qui laisse fructifier l’argent placé sans en toucher les revenus, doubler son capital est affaire de rentabilité et… de temps.

Mais vous ne maîtrisez peut-être pas l’usage de la calculette financière et vous vous crispez à la simple évocation d’une équation avec l’angoisse rétrospective de vos lointains cours de maths.

Heureusement, Albert Einstein vient à notre secours avec sa « règle de 72 » qui donne la méthode de calcul rapide du doublement du capital, et qu’un autre Albert, le Dr. Albert Bartlett, professeur de physique à l’université du Colorado a arrondie à 70, afin de simplifier encore davantage le calcul.

La « fameuse » règle de 70…

Vous voyez, le génial physicien vous réconcilie avec le calcul mental. Vous pouvez maintenant bluffer votre conseiller financier !

Vous voyez également qu’un petit écart dans le taux annuel de placement aboutit à de grandes différences dans les résultats à long terme en particulier si les taux sont élevés.

Rebuté(e) par l’aridité d’un tableau de chiffres, même simplifié, vous serez peut-être plus sensible à l’esthétique de belles courbes.

Le « pouvoir » des intérêts composés 

Ça y est, vous visualisez la courbe des intérêts composés sur une longue période.

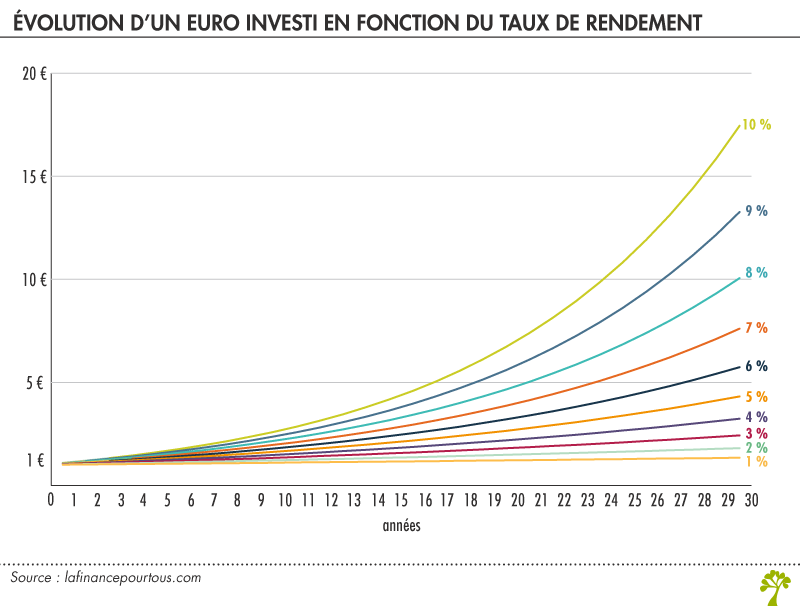
Le graphique ci-dessus montre à quoi ressemble une croissance dite « exponentielle » sur 30 ans à différents taux de rendement, allant de 1 % par an (la ligne la plus basse) à 10 % par an (la ligne la plus haute), d’un euro placé. Les années sont en abscisse (axe horizontale).

• Un rendement stable de 5 % par an signifie que l’on obtient, pour un 1 € placé, 2 € en 14 ans, 2,65 € en 20 ans et 4,33 € après 30 ans.

• Un rendement stable de 10 % par an signifie que l’on obtient, pour un 1 € placé, 2,59 € en 10 ans, 6,72 € en 20 ans et à 17,45 € en 30 ans ! 

La croissance exponentielle est simplement une autre manière de parler du pouvoir des intérêts composés, c’est-à-dire réinvestis avec le capital de départ. 

… Appliquée à un contrat d’assurance vie en euros…

Et maintenant un petit exercice pratique, appliqué à un placement en fonds euro dans un contrat d’assurance vie

Les fonds en euros des contrats d’assurance vie offrent à l’épargnant une garantie du capital investi et l’assurance que les gains passés restent acquis (effet de cliquet).

(Source : FFA et calculs de La Finance pour tous)

Ce placement a bénéficié de rendements importants, notamment au cours des dix premières années. Ce capital investi a doublé en quatorze ans (de 1994 à fin 2008). La règle d’Einstein permet de voir en un clin d’œil, que sur cette période, que le rendement moyen annuel a été de près de 5 % (70 divisé par 14 années).

En revanche, à fin 2020, il aurait fallu investir en 1998 (22 ans) pour obtenir un doublement du capital, ce qui donne un rendement d’environ 3,18 % par an (70 divisé par 22). Ce qui est logique car les rendements des fonds en euros des dernières années sont plus faibles. 

… Et à un placement réalisé sur le Cac 40

Que se passe-t-il si le rendement est négatif certaines années ?

Par définition, les actions cotées en Bourse sont volatiles. Les cours peuvent donc augmenter ou baisser chaque année. 

(Sources : Euronext et calculs de La Finance pour tous)

Continuons l’exercice avec l’indice CAC 40, qui reflète la performance des actions des grandes sociétés françaises cotées. La règle de 70 fonctionne également.

Le CAC 40 « classique » sans dividendes réinvestis

De fin 1995 à fin 2004, en neuf ans, le capital a doublé (1,00 → 2,04) soit un rendement de 70 divisé par 9 = 7,78 % par an.

En revanche, pour obtenir un doublement de son capital à fin 2018, il faut avoir investi début 1996, soit une période de 22 ans à cause des baisses du CAC 40 consécutives à l’éclatement de la bulle Internet en 2001 et 2002) et à la crise des subprimes en 2008. Le rendement d’après la règle d’Einstein nous indique un taux annuel de 3,18 % (70 divisé par 22).

Et le CAC 40 « GR » qui intègre les dividendes

Mais avec l’indice CAC 40 GR (Gross Return) qui intègre les dividendes réinvestis, le constat est différent. On le voit aisément, au fur et à mesure des années d’investissement, le capital a été multiplié par plus de 5 en 24 ans ! C’est assez logique car en plus de la plus ou moins-value annuelle, le résultat intègre les revenus et donc reflète la performance globale des actions.

Attention au point d’entrée

Mais on ne double pas forcément son capital ! En cas d’entrée sur le marché fin 2000 sur le Cac 40 (dividendes non réinvestis), l’investisseur en actions françaises ayant investi 1 euro n’a plus que 94 centimes au bout de 20 années, soit une perte de 6 % de son capital, au 31 décembre 2020.